- Das ontologische Problem: Was ist die genaue Natur dieser außersprachlichen Entitäten?
- Das Problem der Interpretation: Wodurch ist die Interpretationsfunktion genauer bestimmt? [In Vorlesung 5 wird das damit verbundene generelle Problem als Problem der Repräsentation genauer verhandelt]
- Namen ohne realen Bezug: Odysseus.
- Informativität von Sätzen, die referentielle Identität behaupten: Der Morgenstern ist die Venus.
- Was sollen die ‚Benennungsakte' bei Prädikaten, Gattungsnamen u.a. universellen Bezeichnungen sein? Die potentiellen Instanzen lassen sich nicht mehr in endlicher Zeit aufzählen und benennen. [Siehe Universalienproblem]
- Sie bezeichnen etwas (Frege verwendet den in heutiger Sprache leicht zu Mißverständnissen führenden Ausdruck ‚bedeuten etwas')
- Sie drücken einen Sinn aus. Für Eigennamen beispielsweise besteht der Sinn in der Art und Weise, wie der bezeichnete Gegenstand zu identifizieren ist.
- Rudolf Carnap (1956): Meaning and necessity. The University of Chicago Press, Chicago
- Robert Cummins (1991): Meaning and Mental Representation. The MIT Press. Insbes. Abschnitt 8: Interpretational Semantics
- Franz von Kutschera (1993): Sprachphilosophie. Wilhelm Fink Verlag, München. Insbes. Abschn. 2.1: Realistische semantische Theorien.
Was Bedeutungen sind I: die realististische
Antwort
Bedeutung und Interpretation
Eine Bedeutungstheorie ist wesentlich durch
eine Interpretationsfunktion [| ...|] bestimmt, die sprachliche Audrücke
mit gewissen außersprachlichen Entitäten verbindet. [s.
Vorlesung 2]
- Beispiel: Sei eine Domäne D von
Objekten gegeben
[|FIDO|] = Fido
[|IST SATT|] = {x: x ist satt}
Es ergeben sich sofort zwei Probleme:
Kausale Verknüpfung zwischen Namen und Gegenständen, ausgelöst durch „Benennungsakte". Damit wird eine konventionelle Zuordnung gestiftet.
- [|FIDO|] = dasjenige Lebewesen, das „Fido"
genannt wird
[|IST SATT|] = {x: x wird als „satt" bezeichnet}
Drei Problemfälle:
Sprachliche Ausdrücke haben nach Frege zwei Funktionen:
Frege hat versucht, seine Unterscheidung zur Klärung semantischer Sachverhalte in der natürlichen Sprache zu verwenden und hat dabei bahnbrechende analytische Arbeit geleistet. Diese Leistungen wirken bis in die heutige Zeit nach.
So hat Frege indirekte
oder oblique Kontexte untersucht, also Kontexte, die durch gewisse
Einstellungen wie Glaube, Überzeugung, Wünsche, Forderungen etc.
gestiftet werden. In derartigen Kontexten, so Frege, ist die Referenz eines
Ausdrucks als ihr Sinn anzusehen. Unter dieser Annahme kann Frege sein
bekanntes Kompositionalitätsprinzip als universelles Prinzip aufrechterhalten:
Die ‚Bedeutung' (sprich Referenz) eines komplexen Ausdrucks ist
eine Funktion der ‚Bedeutungen' seiner Bestandteile. Als Beispiel betrachte
man den Satz Peter glaubt, daß der Morgenstern die Venus ist.
Der
Wahrheitswert diese Satzes ist abhängig davon, ob der ‚Gedanke' daß
der Morgenstern die Venus ist , eine von Peters Überzeugungen ist.
Der Wahrheitswert hängt also letzendlich nicht allein von der
Referenz
der involvierten Namen Morgenstern und Venus
ab (wie es die
naive Form der realistischen Semantik annimmt), sondern vor allem von deren
Sinn.
| Referenz | Sinn | |
| Eigennamen | Gegenstand | Art des Gegebenseins
(begriffliche, platonische Entität) |
| definite Beschreibungen | identifizierter Gegenstand | kennzeichnender Begriff |
| Prädikate | Begriffsumfang
(damit ist etwas ‚Ungesättigtes' gemeint, also keine ‚Klasse') |
Begriffsinhalt
(platonische Entität) |
| Sätze | Wahrheitswert | Proposition, Gedanke |
Einzuräumen ist, daß der Begriff des Sinns bei Frege in ein gewisses Dunkel gehüllt bleibt. Frege unternimmt nicht ernsthaft den Versuch, etwa Kriterien für Sinngleichheit anzugeben. (Was sind zwei gleiche ‚Arten des Gegebenseins'?). An dieser Stelle leistet Carnaps (1956) Theorie von Intensionen und intensionaler Isomorphie grundlegende Klärungen, die man jedoch nicht als Rekonstruktion von Freges Sinnbegriff verstehen darf, sondern bestenfalls als eine Art von salopper Approximation.
Symbolmanipulation und Interpretation
Die interpretative Semantik geht davon aus,
daß eine Interpretationsfunktion existiert, die den Zusammenhang
zwischen sprachlichen Ausdrücken und außersprachlichen Entitäten
herstellt. Die philosophisch wichtige Frage ist nun, auf welche Weise diese
Interpretationsfunktion näher bestimmt ist. Der einfachste Fall (naive
realistische Semantik) geht davon aus, daß eine direkte kausale Verknüpfung
zwischen Namen und Referenzobjekt (man denke an Taufakte) hergestellt wird.
Durch diese kausale Verknüpfung ist-zumindest für Eigennamen-die
Interpretationsfunktion eindeutig bestimmt. Doch diese Theorie taugt nicht
für Prädikate oder universelle Namen. Freges Theorie läßt
uns ebenfalls im Stich, wenn es um die konkreten Mechanismen geht, die
uns helfen könnten, aus dem Sinn eines Ausdrucks zur Bestimmung seiner
Referenz zu gelangen.
Die moderne interpretative Semantik geht nun von folgender grundsätzlichen Überlegung aus, um den Bereich der potentiell möglichen Interpretationsfunktion drastisch einzuschränken. Zeichen oder Symbole eines symbolmanipulativen Systems stehen nicht isoliert da. Sie sind manipulierbar und treten dadurch in vielfache Beziehungen. Wenn die Symbolmanipulation auf die Simulation der externen Wirklichkeit gerichtet ist, dann stellen die symbolmanipulativen Beziehungen Beschränkungen für die Interpretation bereit. Nach dieser Auffassung können alle wesentlichen Beschränkungen an die Interpretationsfunktionen durch diese symbolischen Verrechnungsverfahren (symbolische Regeln, Prinzipien, Algorithmen etc.) gefaßt werden.
Ein elementares Beispiel für ein symbolmanipulatives System
Seien die symbolischen Strukturen definiert
als Ketten bestehen aus den (elementaren) Symbolen 0 und L. Unser Berechnungssystem
realisiert nun folgende Input-Output-Funktionen auf der Menge S derartiger
Symbolketten:
| F1(x) = z | |
| x | z |
| 0 | L |
| L | L0 |
| L0 | LL |
| LL | L00 |
| L00 | L0L |
| ... | ... |
Allgemein: F1(x0) = xL ; F1(xL) = F1(x)0
Dabei ist x eine Variable für
Symbolketten
| F2(x,y) = z | ||
| x | y | z |
| 0 | 0 | 0 |
| 0 | L | L |
| L | 0 | L |
| L | L | L0 |
| L | L0 | LL |
| ... | ... | ... |
Allgemein: F2(x,0) = x ; F2(x,F1(y)) = F1(F2(x,y))
Dabei sind x und y Variablen für
Symbolketten
Eine Interpretationfunktion für dieses
System ist beispielsweise folgende Funktion, die den Sybolketten natürliche
Zahlen zuordnet:
| [|x|] = n | |
| x | n |
| 0 | 0 |
| L | 1 |
| L0 | 2 |
| LL | 3 |
| L00 | 4 |
| ... | ... |
Die Druckzeichen 0, 1, 2 sollen dabei die Zahlen selber andeuten. Im Unterschied zu den Druckzeichen L,L0, usw., die für Zeichenketten des Symbolsystems stehen (duale Zahlzeichen), stehen die Druckzeichen der ersten Kategorie für reale Objekte (die gemäß Freges Vorstellungen einem ‚drittem Reich'zugehören). Der entscheidende Punkt ist nun, daß die Interpretationsfunktion [|...|] einen Homomorphismus zwischen unserem Berechnungssystem und dem wirklichen Zahlensystem darstellt. Damit ist einfach gemeint, daß die Funktionen F1 und F2 des Berechnungssystems als Funktionen des Zahlensystems gedeutet werden können, und zwar F1 als die Nachfolgerfunktion (Addition von 1) und F2 als die Addition zweier Zahlen:
[|F1(x)|] = [|x|]+1 ; [|F2(x,y)|] = [|x|]+ [|y|]
In mathematischer Sprache ist eine Simulation ganz einfach ein Homomorhismus.
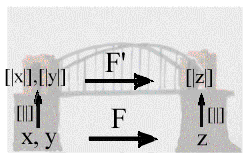 Eine
anschauliche Darstellung des Begriffs der Simulation wird durch das Bild
einer Brücke vermittelt, deren zwei Pfeiler die Interpretationsfunktion
darstellen. Die Grundspanne wird durch die Funktionen der simulierenden
Algebra realisiert und die obere Spanne durch die Funktionen der simulierten
Algebra:
Eine
anschauliche Darstellung des Begriffs der Simulation wird durch das Bild
einer Brücke vermittelt, deren zwei Pfeiler die Interpretationsfunktion
darstellen. Die Grundspanne wird durch die Funktionen der simulierenden
Algebra realisiert und die obere Spanne durch die Funktionen der simulierten
Algebra:
Wir haben gesehen, daß man mit Hilfe eines symbolischen Systems (natürliche) Zahlen simulieren kann.

Von Descartes stammt die Erfindung der analytischen
Geometrie. Die Idee ist, die Punkte der Ebene oder des Raums durch
Zahlenpaare oder Zahlentripel zu simulieren. Damit ist es dann nicht
weit zu der Idee, Kreise und Kugeln durch bestimmte Gleichungen zu simulieren
(x2+y2=r2 für Kreise mit dem
Radius r bzw. x2+y2+z2=r2
für Kugeln mit dem Radius r).
Die Grundidee der interpretativen Semantik ist nun einfach, die Redeweisen a repräsentiert a' bzw. a bedeutet a' durch den technischen Begriff a s-repräsentiert a' zu ersetzen. Mit diesem technichen Begriff von s(imulations)-repräsentiert ist gemeint ist, daß die a enthaltende Algebra die a' enthaltende Algebra simuliert, und zwar mit Hilfe von [|...|]. Dabei wird a auf a' abbildet: [|a|] = a'.
Man könnte nun meinen, daß die Interpretationsfunktion im Idealfall durch die genannten Korrespondenzbedingungen eindeutig bestimmt ist. Nur wenn dies der Fall ist, kann man beispielsweise im Falle eines symbolverarbeitenden Systems A gerechtfertigt davon sprechen, daß A aus sich heraus (mit Hilfe der Korrespondenzbedingungen) etwas bestimmtes repräsentiert. Im anderen Falle braucht man einen zusätzlichen Mechanismus, vielleicht in Form eines Guten Willens oder eines referenzstiftenden Dämons, der diese Aufgabe leistet.
Es ist nicht schwer, die Einsicht zu erlangen,
daß die Idee der Simulation (oder des Homomorphismus) nicht ausreichend
ist, die gewünschte Eindeutigkeit der Interpretationsfunktion zu erlangen.
Entsprechende Überlegungen mögen Frege dazu gebacht habe, dieses
im engen Zusammenhang zu Hilberts sogen. axiomatische Methode (Hilbertsche
Methode) stehendes Verfahren als Verfahren zur Bedeutungsbestimmung abzulehnen.
Und Putnam haben derartige Überlegung davon überzeugt, seinen
‚metaphysischen Realismus' aufzugeben.
Literatur: